Minimum Spanning Tree

What is a Spanning Tree?

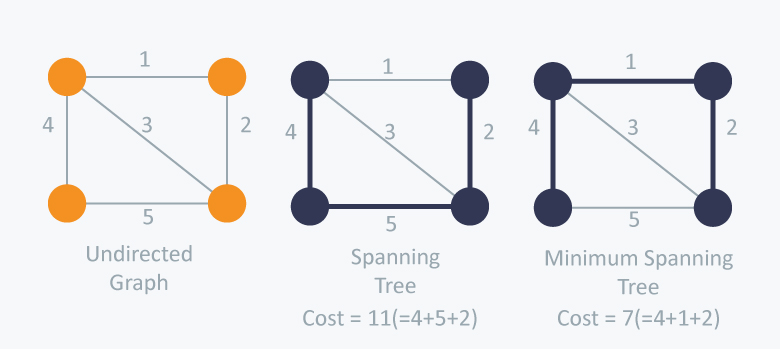
Given an undirected and connected graph $G=(V,E)$, a spanning tree of the graph $G$ is a tree that spans $G$ (that is, it includes every vertex of $G$) and is a subgraph of $G$ (every edge in the tree belongs to $G$)

What is a Minimum Spanning Tree?

The cost of the spanning tree is the sum of the weights of all the edges in the tree. There can be many spanning trees. Minimum spanning tree is the spanning tree where the cost is minimum among all the spanning trees. There also can be many minimum spanning trees.

Minimum spanning tree has direct application in the design of networks. It is used in algorithms approximating the travelling salesman problem, multi-terminal minimum cut problem and minimum-cost weighted perfect matching. Other practical applications are:

1. Cluster Analysis
2. Handwriting recognition
3. Image segmentation     

There are two famous algorithms for finding the Minimum Spanning Tree:

Kruskal’s Algorithm

Kruskal’s Algorithm builds the spanning tree by adding edges one by one into a growing spanning tree. Kruskal's algorithm follows greedy approach as in each iteration it finds an edge which has least weight and add it to the growing spanning tree.

Prim’s Algorithm

Prim’s Algorithm also use Greedy approach to find the minimum spanning tree. In Prim’s Algorithm we grow the spanning tree from a starting position. Unlike an edge in Kruskal's, we add vertex to the growing spanning tree in Prim's.